
The endothelial glycocalyx, a highly hydrated mesh of membra ne-bound negatively charged proteoglycans, glycosaminoglycans, glycoproteins, and glycolipids, has a thickness of around 500 nm (see figure 1). This layer shields the endothelial cells from the flowing blood and forms a barrier between the plasma constituents and the underlying cells. To understand more about its viscoelastic properties we can use a tool called “optical tweezers”.
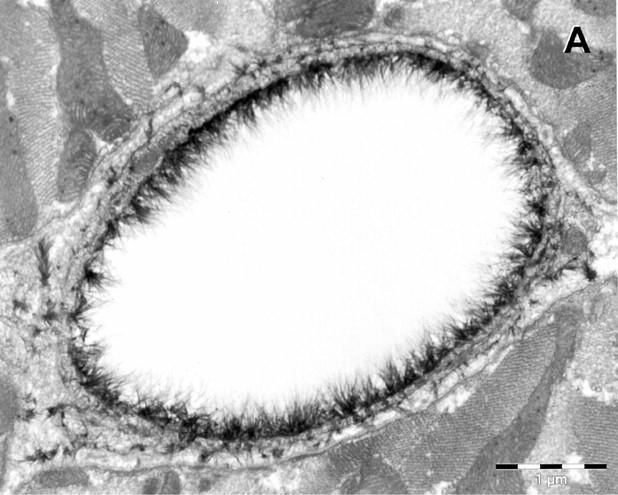
Figure 1. Electron microscope overview of an Alcian blue 8GX-stained rat left ventricular myocardial capillary (bar=1mm). The “hairy” structures form the endothelial glycocalyx. Figure taken from Van den Berg, Vink, Spaan, Circulation Research 2003, 92: 592-594
With a focused laser beam, dielectric particles of sizes ranging from nanometers to micrometers, can be trapped. Apart from being strongly focused, the beam should also have a Gaussian profile. This means that its intensity is the highest in the center of the beam (see figure 2). To get a strongly focused laser beam, a microscope with a high numerical aperture (NA) is used. This set-up is called an "optical tweezers".
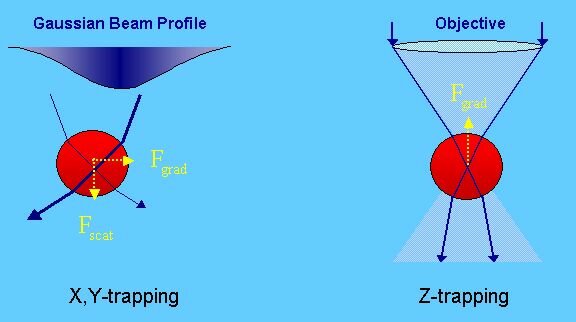
Figure 2. 3-dimensional trapping of a bead by a laser beam with a Gaussian beam profile. The beam is focused by a high numerical aperture objective. X,Y-trapping (lateral) is due to the gradient force, that points to the high intensity part of the laser beam. Z-trapping (axial) is due to the gradient force which points in the direction of the focal point, and in the opposite direction of the scattering force.
Trapping is possible due to the fact that the incident laser light is deflected by the particle, causing a radiation pressure on the particle. This results in two forces: a gradient, and a scattering force. The gradient force is responsible for pushing the particle back to the center of the beam (highest intensity)(x, y-direction). The scattering force pushes the particle along the direction of the propagation of the laser light. Since the objective lens has a high NA, there will also be a steep gradient in the z-direction, which causes a gradient force in the direction of the focal point of the lens. This force opposes the scattering force, and thus the particle is trapped within three dimensions (see figure 2).
When we trap a small bead, and bring it into the glycocalyx, the bead will move within the trap due to the thermal motion of the molecules composing the glycocalyx. This Brownian motion can be measured, and a power spectrum of the bead fluctuations can be obtained. From this spectrum the complex shear modulus G* is calculated. G* has two components: the storage modulus (the real part of G*) and the loss modulus (the imaginary part of G*). The former is a measure for the elasticity of the material, the latter is a measure for its viscosity. Thus by measuring the Brownian motion of a bead embedded in the glycocalyx, we can tell something about its viscoelastic properties.
Hi, my name is Nadja Nijenhuis. I am a PhD. student at the department of Medical Physics of the University of Amsterdam. Before starting in 2003 on the work described above, I studied Experimental Physics at the University of Amsterdam, with a specialization in High Energy Physics. My thesis was about the time characteristics of the photomultiplier that is going to be used by the ANTARES experiment.
![]()